题解 P5513 [CEOI2013] Board
懂不懂什么叫 $O(\frac{n^2}{\omega})$ 啊。
题意
思路
首先给每个节点编个号,类似于线段树,设当前节点为 $x$,则左儿子为 $2x$,右儿子为 $2x+1$。
这样我们就能用一个二进制数表示每个节点的位置。
并且容易发现,点 $x$ 和点 $y$ 之间的最短路为:
$$ \min\limits_{a,b}{ (\lvert\lfloor\frac{x}{2^a}\rfloor-\lfloor\frac{y}{2^b}\rfloor\rvert+a+b)[h(\lfloor\frac{x}{2^a}\rfloor)=h(\lfloor\frac{y}{2^b}\rfloor })] $$
$h(x)$ 表示 $x$ 的最高二进制位在第几位。
很抽象?说人话就是将 $x,y$ 向上跳到同一高度后,他们的之间的差的绝对值取最小值。
图示:
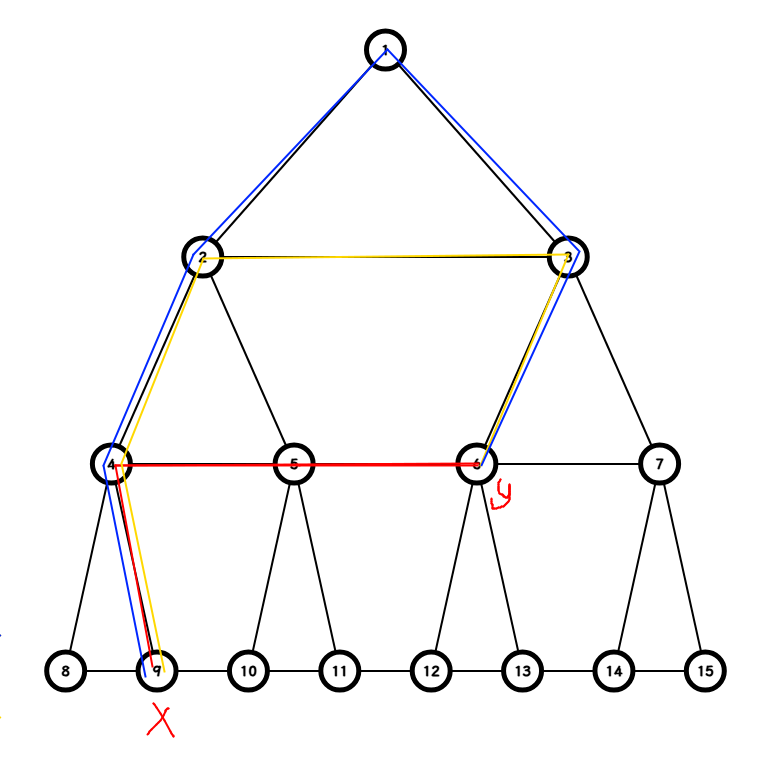
三条线即为 $x,y$ 之间最短路的三种可能取值。
计算答案流程就是:
假设 $x$ 大于 $y$。
先将 $x$ 向上跳至和 $y$ 同一高度,然后计算 $x$ 和 $y$ 的差。
再把 $x$ 和 $y$ 同时向上跳一个父亲。
重复上面操作直到 $x,y$ 重合。
关于处理 $x,y$ 位置,只需要处理几种操作分别是向哪里转移,模拟即可。
但是还有一个问题:$x,y$ 的最大值为 $2^{10^5}$,这存不下。
所以要使用高精度。
但是普通的高精是 $O(n^2)$ 的,不能通过。
于是我们可以参考一下 bitset,将多个进制位用同一个数存下即可。
时间复杂度 $O(\frac{n^2}{\omega})$,$\omega$ 取 $60$ 即可。
code
#include<cstring>
#include<iostream>
using namespace std;
const int N=61;
struct BYDSET//普通压位高精
{
long long a[2005];
int L;
BYDSET(){L=0;memset(a,0,sizeof(a));}
void rmove()
{
for(int i=L;~i;i--)
{
a[i]<<=1;
if(a[i]&(1ll<<(N+1)))a[i+1]|=1,a[i]^=(1ll<<(N+1));
}
if(a[L+1])L++;
}
void lmove()
{
for(int i=0;i<=L;i++)
{
if((a[i]&1)&&i)a[i-1]|=(1ll<<N);
a[i]>>=1;
}
if(!a[L]&&L)L--;
}
void push()
{
a[0]++;
for(int i=0;i<=L;i++)
{
if(a[i]>=(1ll<<(N+1)))
{
a[i]-=(1ll<<(N+1));
a[i+1]++;
}
else break;
}
if(a[L+1])L++;
}
void idk()
{
a[0]--;
for(int i=0;i<=L;i++)
{
if(a[i]<0)
{
a[i]+=(1ull<<(N+1));
a[i+1]--;
}
else break;
}
if(!a[L]&&L)L--;
}
int highbit()
{
for(int i=N;~i;i--)if(a[L]&(1ull<<i))return i+L*(N+1);
return -1;
}
void operator=(BYDSET const&s)
{
L=s.L;
for(int i=0;i<=L;i++)a[i]=s.a[i];
}
BYDSET operator-(const BYDSET&s)const
{
BYDSET ans;
for(int i=0;i<=L;i++)ans.a[i]=a[i];
ans.L=L;
for(int i=0;i<=L;i++)
{
ans.a[i]-=s.a[i];
if(ans.a[i]<0)
{
ans.a[i]+=(1ll<<(N+1));
ans.a[i+1]--;
}
}
while(!ans.a[ans.L]&&ans.L)ans.L--;
return ans;
}
}A,B,C;
int cmp(BYDSET a,BYDSET s)
{
int A=a.highbit(),S=s.highbit();
if(A!=S)return A>S;
for(int i=a.L;~i;i--)if(a.a[i]!=s.a[i])return a.a[i]>s.a[i];
return 2;
}
long long ask()
{
long long ans=0;
int AA=A.highbit(),BB=B.highbit();
if(AA<BB)swap(A,B),swap(AA,BB);
while(AA>BB)ans++,A.lmove(),AA--;
int o=cmp(A,B);
if(o==2)return ans;
if(!o)swap(A,B);
BYDSET C=A-B;//C为x与y的差值
int CC=C.highbit();
long long num=0,an=1e10;
o=0;
while(1)
{
C=A-B;
CC=C.highbit();
if(!~CC)break;
o=1;
if(!C.L)an=min(num+(long long)C.a[0],an);
//当C的位数大于60时是绝对不优的,不用加入贡献
A.lmove();
B.lmove();
num+=2;
}
return ans+an*o;
}
char a[200005],b[200005];
int n,m;
int main()
{
scanf("%s%s",a+1,b+1);
n=strlen(a+1);
m=strlen(b+1);
A.a[0]=1;
B.a[0]=1;
for(int i=1;i<=n;i++)//处理x最后的位置
{
if(a[i]=='1')A.rmove();
else if(a[i]=='2')A.rmove(),A.push();
else if(a[i]=='U')A.lmove();
else if(a[i]=='L')A.idk();
else A.push();
}
for(int i=1;i<=m;i++)//同上
{
if(b[i]=='1')B.rmove();
else if(b[i]=='2')B.rmove(),B.push();
else if(b[i]=='U')B.lmove();
else if(b[i]=='L')B.idk();
else B.push();
}
printf("%lld",ask());
}