题解 CF1368H2 Breadboard Capacity (hard version)
有趣。
以及要分清反轉和翻轉。
题意
试验板有 $n$ 行 $m$ 列,每个行列交叉处有一个节点。试验板每侧都有端口。左、右侧各 $n$ 个端口,上、下侧各 $m$ 个端口。每个端口是红色或蓝色。
端口可通过导线连接。
-
每根导线连接一红色端口和一蓝色端口,每个端口最多连一条导线。
-
导线的每个部分水平或垂直。
-
导线不能在节点之外的地方和其他导线相交(也不可以和自己相交)。
试验板的容量是根据上述规则导线数量的最大值。
端口颜色未固定,有 $q$ 次修改。每次修改,在一条边上的连续区间内,端口颜色反转。
计算每次修改后试验板容量。
思路
首先使用网络流。
将蓝色连原点,红色连汇点,交叉处的点向四联通连点,容量均为 $1$。
但是由于点数是 $n^2$ 级别的,网络流无法通过。
于是就可以借助模拟网络流。
因为最大流等于最小割,问题就转化为了给格子进行红蓝染色,代价为红蓝接壤的边界长度,求最小代价。
好,开始找性质。
- 如果出现一条边界连接了同一个或相邻的边,那么我们可以改变点的颜色使这样的边界消失并且答案不会变得更劣。
如图(来自官方题解):
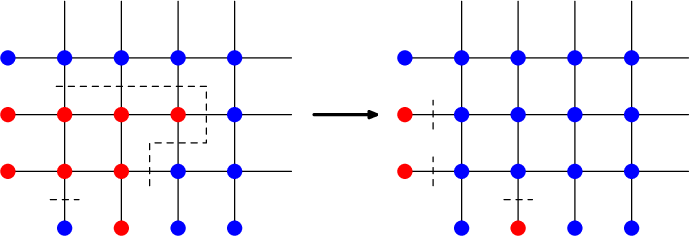
一个比较感性的理解是:经过这次操作后这条边界的矩形内部的部分会消失,而与矩形边长相交的部分可能会增加,但是由于内部部分边长一定大于等于外部部分边长,所以这样操作是绝对不劣的。
- 如果边界上的路径出现了折线,那么我们完全可以将它捋直并且答案不会变得更劣。
如图(来自官方题解):
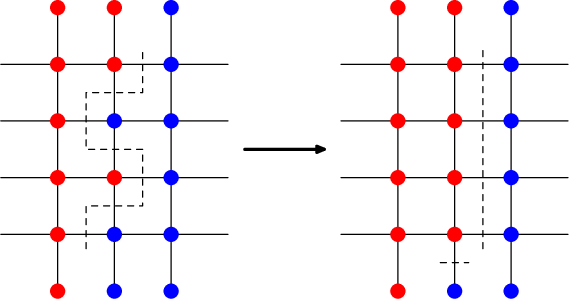
证明比较显然,故省略。
于是问题变成了从上到下或从左到右一层一层染色,求最小代价。
一个很显然的 DP,转移方程如下($0,1$ 各代表一种顏色):
$$
\begin{cases}
f_{i,0}=\min(f_{i-1,0},f_{i-1,1}+m)+[L_i=0]+[R_i=0] \\
f_{i,1}=\min(f_{i-1,1},f_{i-1,0}+m)+[L_i=1]+[R_i=1]
\end{cases}
$$
对于修改,可以考虑使用动态 DP。
做法是对于每个位置开四个矩阵,存储左边变、右边变、不变和都变这四种情况。
每次修改操作时交换两对矩阵即可。
另一个方向同理。
时间复杂度 $O(n\log n)$。
code
#include<cstring>
#include<iostream>
#define mp(x,y) make_pair(x,y)
using namespace std;
const int sz=2;
struct mat
{
int a[sz][sz];
mat(){memset(a,0,sizeof a);}
mat operator*(const mat& T)const
{
mat res;
int r;
for(int i=0;i<sz;i++)for(int j=0;j<sz;j++)res[i][j]=1e9;
for(int i=0;i<sz;i++)
for(int k=0;k<sz;++k)
{
r=a[i][k];
for(int j=0;j<sz;j++)res.a[i][j]=min(res.a[i][j],T.a[k][j]+r);
}//广义矩乘
return res;
}
int* operator[](int x)
{
return a[x];
}
};
char s[4][1000005];
int n,m;
struct Segment_Tree
{
struct sss
{
int l,r,num1,num2,tag1,tag2;
mat sum,insum,vsum,invsum;
#define l(x) tree[x].l
#define r(x) tree[x].r
#define sum(x) tree[x].sum
#define vsum(x) tree[x].vsum
#define insum(x) tree[x].insum
#define invsum(x) tree[x].invsum
#define num1(x) tree[x].num1
#define num2(x) tree[x].num2
#define tag1(x) tree[x].tag1
#define tag2(x) tree[x].tag2
}tree[1000005];
void pushup(int x)
{
sum(x)=sum(x*2)*sum(x*2+1);
vsum(x)=vsum(x*2)*vsum(x*2+1);
insum(x)=insum(x*2)*insum(x*2+1);
invsum(x)=invsum(x*2)*invsum(x*2+1);
num1(x)=num1(x*2)+num1(x*2+1);
num2(x)=num2(x*2)+num2(x*2+1);
}
void build(int x,int l,int r,int p)
{
l(x)=l;r(x)=r;
if(l(x)==r(x))//构建四个矩阵
{
int o=0,y=m;
if(p)o=2,y=n;
sum(x)[0][0]=sum(x)[1][0]=(s[o][l]=='R')+(s[1+o][l]=='R');
sum(x)[0][1]=sum(x)[1][1]=(s[o][l]=='B')+(s[1+o][l]=='B');
sum(x)[1][0]+=y;
sum(x)[0][1]+=y;
vsum(x)[0][0]=vsum(x)[1][0]=(s[o][l]!='R')+(s[1+o][l]=='R');
vsum(x)[0][1]=vsum(x)[1][1]=(s[o][l]!='B')+(s[1+o][l]=='B');
vsum(x)[1][0]+=y;
vsum(x)[0][1]+=y;
insum(x)[0][0]=insum(x)[1][0]=(s[o][l]=='R')+(s[1+o][l]!='R');
insum(x)[0][1]=insum(x)[1][1]=(s[o][l]=='B')+(s[1+o][l]!='B');
insum(x)[1][0]+=y;
insum(x)[0][1]+=y;
invsum(x)[0][0]=invsum(x)[1][0]=(s[o][l]!='R')+(s[1+o][l]!='R');
invsum(x)[0][1]=invsum(x)[1][1]=(s[o][l]!='B')+(s[1+o][l]!='B');
invsum(x)[1][0]+=y;
invsum(x)[0][1]+=y;
num1(x)=s[o][l]=='R';
num2(x)=s[o+1][l]=='R';
return;
}
int mid=(l+r)>>1;
build(x*2,l,mid,p);
build(x*2+1,mid+1,r,p);
pushup(x);
}
void flip(int x,int p)//反转操作
{
if(!p)
{
swap(sum(x),vsum(x));
swap(insum(x),invsum(x));
num1(x)=r(x)-l(x)+1-num1(x);
tag1(x)^=1;
}
else
{
swap(sum(x),insum(x));
swap(vsum(x),invsum(x));
num2(x)=r(x)-l(x)+1-num2(x);
tag2(x)^=1;
}
}
void spread(int x)
{
if(tag1(x))
{
flip(x*2,0);
flip(x*2+1,0);
tag1(x)=0;
}
if(tag2(x))
{
flip(x*2,1);
flip(x*2+1,1);
tag2(x)=0;
}
}
void change(int x,int l,int r,int p)
{
if(l<=l(x)&&r(x)<=r)return flip(x,p);
spread(x);
int mid=(l(x)+r(x))>>1;
if(l<=mid)change(x*2,l,r,p);
if(mid<r)change(x*2+1,l,r,p);
pushup(x);
}
mat ask(){return sum(1);}
int cnt(int p){return p?num2(1):num1(1);}
}T1,T2;
int calc(pair<int,int>M1,mat M2,pair<int,int>M3)
{//计算答案
pair<int,int>res(-1e9,-1e9);
res.first=min(M1.first+M2[0][0],M1.second+M2[1][0]);
res.second=min(M1.first+M2[0][1],M1.second+M2[1][1]);
res.first+=M3.first;
res.second+=M3.second;
return min(res.first,res.second);
}
int work(){return min(calc(mp(T1.cnt(0),m-T1.cnt(0)),T2.ask(),mp(T1.cnt(1),m-T1.cnt(1))),calc(mp(T2.cnt(0),n-T2.cnt(0)),T1.ask(),mp(T2.cnt(1),n-T2.cnt(1))));}
int T;
int main()
{
scanf("%d%d%d",&n,&m,&T);
for(int i=0;i<4;i++)scanf("%s",s[i]+1);
T1.build(1,1,m,1);
T2.build(1,1,n,0);
printf("%d\n",work());
while(T--)
{
char op[1];
int l,r;
scanf("%s%d%d",op,&l,&r);
if(op[0]=='U')T1.change(1,l,r,0);
else if(op[0]=='D')T1.change(1,l,r,1);
else if(op[0]=='L')T2.change(1,l,r,0);
else T2.change(1,l,r,1);
printf("%d\n",work());
}
}
/*
dp_{i,0}=min(dp_{i−1,0},dp_{i−1,1}+m)+[L_i=0]+[R_i=0]
dp_{i,1}=min(dp_{i−1,0}+m,dp_{i−1,1})+[L_i=1]+[R_i=1]
*/
/*
*/